AREAS OF KNOWLEDGE:
MATHEMATICS
THIS STATEMENT IS FALSE
![One version of the Liar's paradox first described by Zeno of Elea [495-430 BC]](https://images.squarespace-cdn.com/content/v1/59038f2c440243a0d4b45f4c/1499957608091-Z6T72IDE16ELDS431NBF/image-asset.jpeg)
One version of the Liar's paradox first described by Zeno of Elea [495-430 BC]
CLASS ACTIVITY I: THE LIAR'S PARADOX
Certain logical conundrums, like this version of the liar's paradox, sabotage conventional ideas of absolute certainty, and perfect consistency, in the edifice of pure mathematics.
After the initial discomfort generated by this mind-bending paradox fades, and students see for themselves that this is not a puzzle of logic easily resolved, some lively interchange will ensue. The following guiding questions may or may not add value.
Well, is the statement true or false?
This is a self-referential statement? What is self-referentiality and why is it problematic here?
We commonly associate the analytical realms of pure mathematics and logic with certainty. To what extent does the existence of occasional paradoxical results undermine the assumption of certainty?
THE BARBER'S PARADOX
Old photo of the Frantz Barber Shop, Anaheim, CA.
Continue the class conversation with: If Barbers are those who shave men if and only if they do not shave themselves, do barbers shave themselves? Ask students what they think? Of course, a contradiction is soon reached; but just saying the barber in question must be a woman who does not shave, or the that the sentence just doesn't make sense, are shrewd responses, but they just jump out of dealing with the paradox.
Inform students that at the beginning of the 20th Century, famous mathematicians (including Russell, Whitehead, Frege and Hilbert) were aiming for a rock solid foundation for the whole of mathematics based on logical certainty. Paradoxes undermined their towering ambition, and in 1930 such noble but, ultimately, hubristic attempts were permanently laid to rest by Gödel's famous Incompleteness Theorem.
The following quotes are very revealing and students should be told to keep them in mind when tackling the Platonists vs. Formalists written assignment which follows this unit.
“I wanted certainty in the kind of way in which people want religious faith. I thought that certainty is more likely to be found in mathematics than elsewhere. But I discovered that many mathematical demonstrations, which my teachers expected me to accept, were full of fallacies, and that, if certainty were indeed discoverable in mathematics, it would be in a new field of mathematics, with more solid foundations than those that had hitherto been thought secure. But as the work proceeded, I was continually reminded of the fable about the elephant and the tortoise. having constructed an elephant upon which the mathematical world could rest, I found the elephant tottering, and proceeded to construct a tortoise to keep the elephant from falling. But the tortoise was no more secure than the elephant, and after some twenty years of very arduous toil, I came to the conclusion that there was nothing more that I could do in the way of making mathematical knowledge indubitable.”
“The goal of my theory is to establish once and for all the certitude of mathematical methods… The present state of affairs where we run up against the paradoxes is intolerable. Just think, the definitions and deductive methods which everyone learns, teaches and uses in mathematics, the paragon of proof and certitude, lead to absurdities! If mathematical thinking is defective, where are we to find truth and certitude? ”
Einstein and Gödel on one of their regular walks in Princeton, New Jersey.
CLASS ACTIVITY II: NON-EUCLIDEAN GEOMETRY
Remind students that all of Euclidean geometry is built on five self-evident axioms and postulates. Over the centuries it became apparent that proving Euclid’s fifth postulate (the postulate of parallels) was problematic. Recognizing that the postulate of parallels was not as self-evident as the other four postulates, led to the discovery of non-Euclidean geometry, in which the parallel postulate is assumed to be false.
Hyperbolic non-Euclidean surfaces are convex and saddle-shaped. Parallel lines converge. Elliptic non-Euclidean surfaces are concave. Parallel lines diverge. A familiar example is the surface of a sphere.
How the sum of the angles of a triangle differs in non-Euclidean geometries.
HANDS ON TASK WITH A REAL GLOBE
For this "hands-on" activity students should work in trios. Well in advance of the class arrange to have on hand sets of school globes, rulers, string, tape and protractors.
1. Lead students through the following thought experiment:
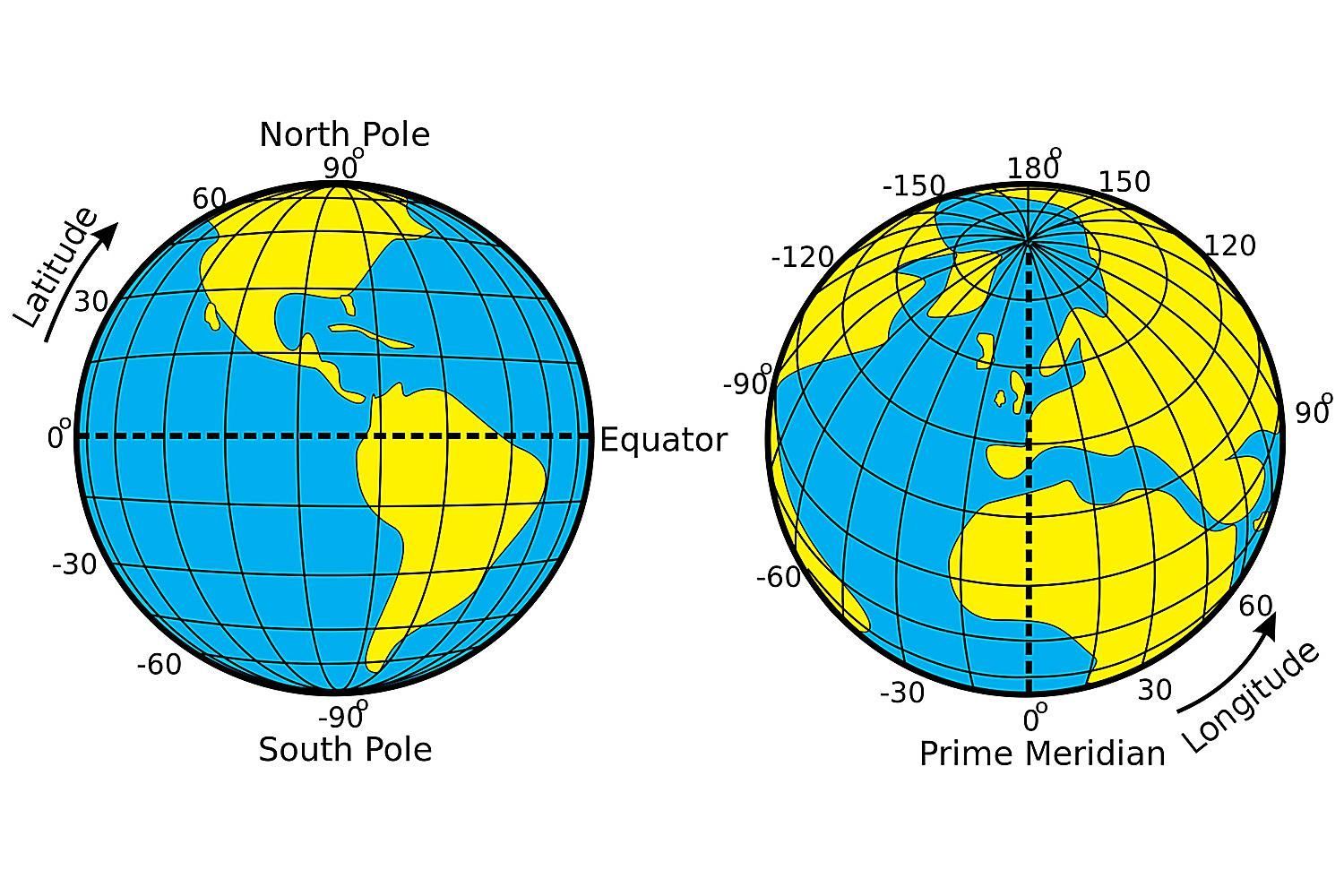
First ensure that you know the difference between lines of latitude and lines of longitude. The most famous line of latitude is the equator. All the other lines of latitude are parallel to the equator and get smaller as they approach the poles. The lines of longitude are all "great circles" like the equator and pass through the North and South poles. The lines of longitude are conventionally 15 degrees apart. Why?
Djexplo / Wikimedia Commons
Imagine a line of longitude intersecting with the equator. What is the size of the angle formed? Now mentally shift around the equator to where the next line of longitude intersects with the equator. Again what is the size of the angle formed between them? Next, picture in your mind an isosceles triangle with a base that is the portion of the equator between two lines of longitude fifteen degrees apart. The sides of the triangle are precisely the two lines of longitude which converge the further away they get from the base, eventually intersecting at the North pole forming an angle of 15 degrees. What is the sum of the angles of the triangle?
2. On a globe mark 3 random crosses on three different continents, (to allow significant distance between them). Use a stretched string and tape to define the triangle made by joining up the points. Use a protractor to measure carefully sum of the angles of the triangle.
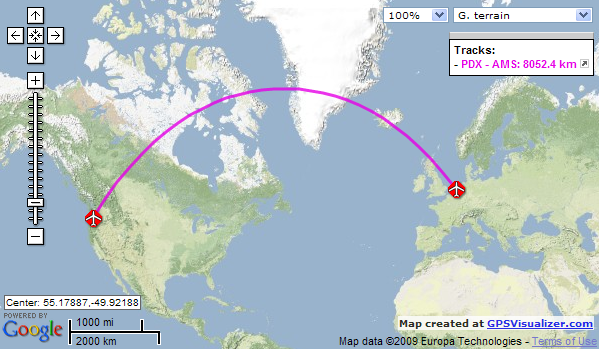
3. First choose your favorite European city. Next identify two different flight paths between San Francisco and your chosen destination based on the Google map above
A. Going directly West to East.
B. Going East to West but veering North along the way, so you go over arctic Canada Greenland and Iceland.
Use stretch string and tape to mark the two journeys. Finally using a ruler measure the two lengths of string that you used.
CLASS ACTIVITY III: INFINITIES
Have you encountered aleph zero before? It represents the smallest infinity: the infinite number of counting (cardinal) numbers!
This activity consists of nothing more than observing a humorous video about the Hilbert Hotel which seems to have infinite possibilities. Invite students to respond to the Toy Story graphic. Like logical paradoxes and non-Euclidean geometries, the counterintuitive consequences of infinities will inform the Platonists vs. Formalists written assignment which will be the culmination of our brief meta-view of mathematics as an Area of Knowledge.
Why specifically is this hilarious and much quoted line from Pixar's Toy Story movie not even wrong?
The dismissive phrase "not even wrong" originated with physicist Wolfgang Pauli in response to pseudoscientific claims that contain erroneous logic or cannot be falsified by experiment.